Build a lane change decision model with Compact Support Neural Network
Introduction
The current mainstream Planning & Control (P&C) algorithm for Autonomous Vehicle (AV) is rule-based. There are lots of redundancy in the system and AV is overly defensive in scenarios need interaction with other road users, e.g., lane change, merge, unprotected left turn, roundabouts, etc. Indecisiveness will confuse other road users and block traffic. We propose to use data-driven approach to learn the human driver’s mental model in lane change decision making.
Deep learning has very successful applications in object classification, language translation, game playing and many others, but it’s overconfident in its application (see paper here) In out-of-distribution (OOD) samples, it will still confidently output a prediction, i.e., it does not know when it’s unknown. 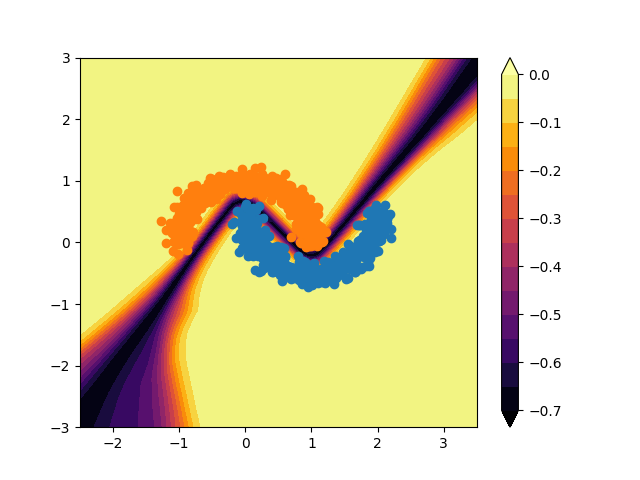
A Multi-layer Perceptron (MLP) Neural Network (NN) is trained on the Moon dataset. As we can see in the figure, NN has very high confidence in OOD samples far from its training dataset.
If we want to apply NN to P&C of AV industry, we must be able to assess the confidence in our prediction, as one decision can be a matter of life and death. When the confidence is low and uncertainty is high, a conservative action should be pursued.
Compact Support Neural Network (CSNN)
We propose the Compact Support Neural Network (CSNN), in which neuron will have a compact support and NN can output zero confidence for OOD samples. The activation of neuron is defined as \begin{eqnarray} f( x)&=&\max(R^2-|| x- \mu||^2,0) \nonumber \ &=&\max(\alpha(R^2- x^T x- \mu^T \mu)+2 \mu^T x,0) \end{eqnarray} When $\alpha=0$, it will be a standard ReLU neuron, and when $\alpha>0$, it will be a Compact Support Neuron. It can be shown that the neuron only has support within a ball of radius \begin{eqnarray} R_\alpha^2=R^2+||\mu||^2(\frac{1}{\alpha^2}-1) \end{eqnarray} and center \begin{equation} c=\frac{\mu}{\alpha} \end{equation}
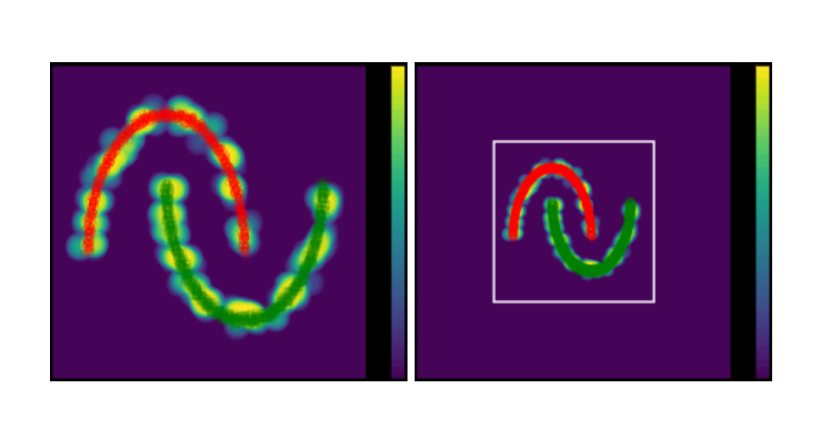
As we can see in the figure, with compact support, the NN output almost 0 confidence when samples are far from training dataset.
Experiments
NGSIM dataset and OOD samples
We train the CSNN algorithm on the NGSIM I80 dataset, which is a 45-minute video recoding of a 500-meter long highway. We extracted all the lane changes and labeled them into 3 categories:
- Cooperative. Ego (i.e., the agent which carries out lane change) changes lane and does not cause a harsh brake for the lag vehicle in target lane.

- Adversarial. Ego changes lane and causes a harsh brake for the lag vehicle in target lane.

- Adversarial. Ego aborts the current window due to competition and chooses to change lane in the next window.

We then generate the OOD samples with uniform sampling. Overall, 153509 OOD samples are generated and there are 1584 in-distribution samples. 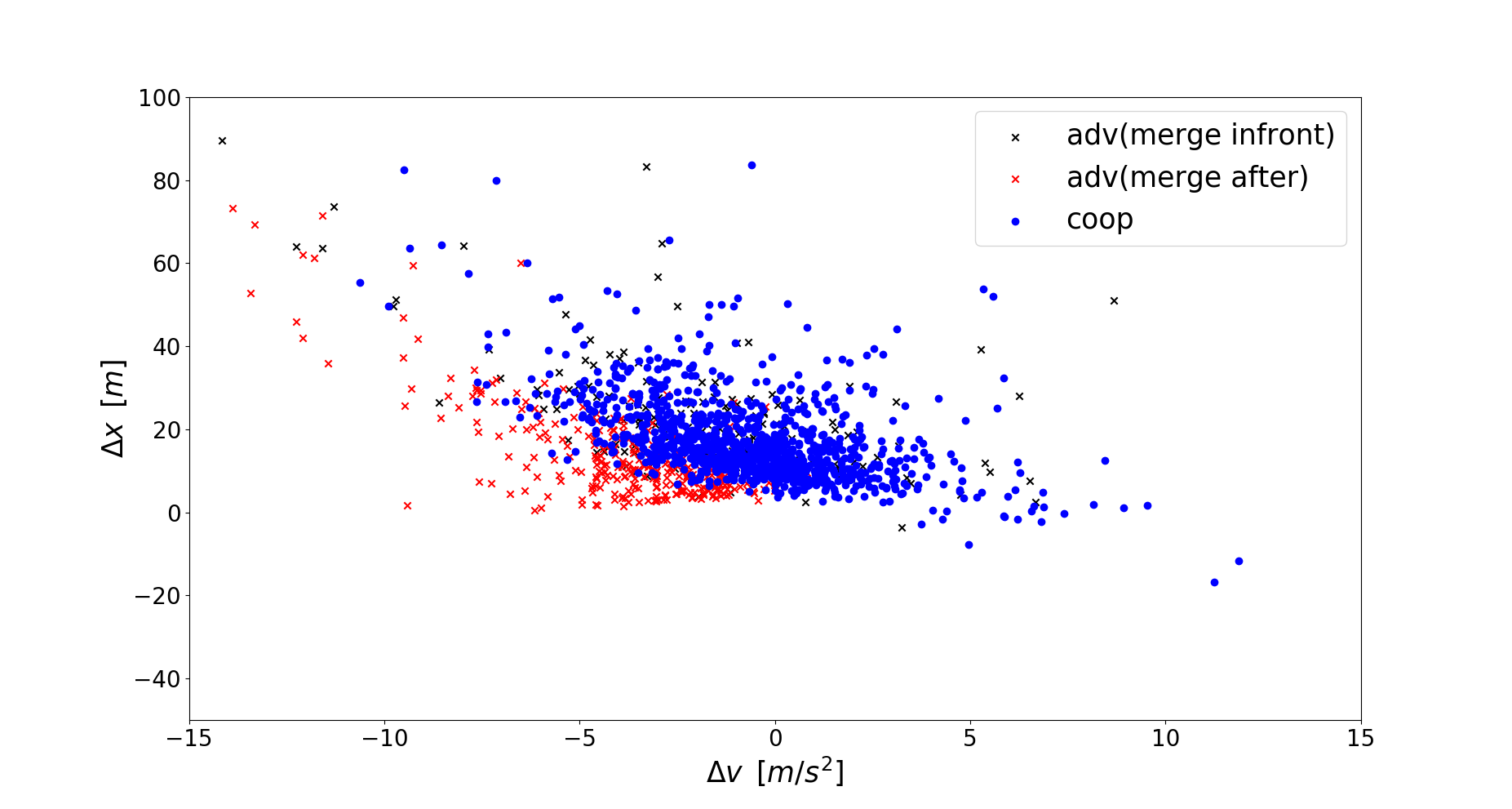
Model
A network of:
- A fully connected layer with 64 neurons and $reLU$ activation
- Batch normalization layer without affine learning, i.e., normalize the output of previous layer such that they have 0 mean and 1 standard deviation.
- A fully connected layer with 64 Compact Support Neurons with hyperparameter $r=1$.
- Output layer with 2 heads.
Results
The model has obtained accuracy 0.833 and AUC of 0.99 when $\alpha=0.325$, which is better than the state-of-the-art result, i.e., result using deterministic uncertainty quantification (DUQ), which has best result of accuracy 0.824 and AUC of 0.98. Another popular method in detecting OOD samples, deep ensemble, completely failed in this task. A ensemble of 5 NN has AUC of 0.396, we suspect in low-dimension space, the individual network tends to agree with each other on the OOD samples and the entropy of prediction is low instead of high. 
Conclusion
The Compact Support Neural Network can have the same prediction accuracy for in-distribution samples compared with classifiers trained with normal neurons and beat state-of-the-art results in detecting OOD samples. It can be a great algorithm to detect long-tail rare events.
